
HexDome
Hexagonal Geodesic Domes
Minimal stable system
Immobilization with seven cables
The smallest number of cables I have managed to find which will stabilise an
object in three dimensions is seven.
Here is a tetrahedron stabilised by seven cables.

Immobilization with seven cables
|
The sides of the triangle are in the same plane as the
anchors. This doesn't lead to the greatest restoring forces
- but it does make it easy to demonstrate stability by
resolving forces and taking moments around the triangle's
apex.

Magnetic model
|
The next two diagrams here illustrate another model. It is
shown from two different directions.

Stability with seven cables (bottom view)
|
|

Stability with seven cables (top view)
|
A fairly simple argument is sufficient to demonstrate the
stability of this system.
- The central point of the hexagon behaves as though
constrained by four cables, leading to each anchor point.
That is sufficient to fix its coordinates in space.
- Each of the three pairs of cables connected to the
ground removes precisely one of the remaining degree of
rotational freedom from the system.
Magnetic model

Magnetic model
|
|

Magnetic model
|
These models are provided to help visualise the structure.
Because the cables in this model can actually sustain
compressive forces, the model isn't intended to be
an accurate representation of the system.

Magnetic model
|
Notice that the hexagon is twisted with respect to its
supports. This allows the cables to cross by each other
without touching.
Removing translational degrees of freedom
Here's a diagram of four cables taking away all the
translational degrees of freedom of a
tetrahedron.

Removing translational freedoms
The centre of gravity of the tetrahedron is effectively
immobilised, though the tetrahedron is still free to twist
on a small scale.
This is a well-known, classical configuration.
Removing rotational degrees of freedom
Here's a diagram of five cables taking away all the
rotational degrees of freedom of a white triangle -
which has already had its translational freedoms
removed.
Please note that the red node marked "O" is considered to be
fixed in space in this diagram.
The triangle would be free to rotate about it - were it not
attached to the anchors (marked A-E) by the five horizontal
cables.
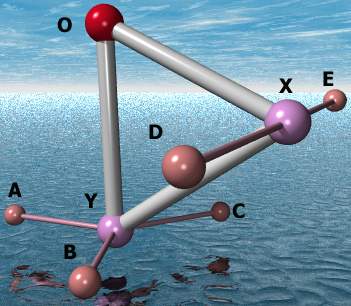
Removing rotational freedoms
My first attempt at solving this problem remains visible
here.
Under some circumstances, as well as immobilising an object,
it is desirable to apply as few torques as possible to the
object.
Fixing an object in space with no torque at all is only
possible in free fall.
Assuming free fall conditions, the following diagram
attaches nine cables to four points on a white triangle -
in such a way that the object is immobilised - and the
resultant of the externally-applied forces at each
point is zero.
If the object is not in free fall such a configuration would
minimize the applied torques.

9 cables - minimal torque
Note that this configuration is a simple combination of the
last two diagrams.
My first attempt at solving this problem remains visible
here.
Immobilization with six struts
Another related question is: how many struts are
needed to immobilise a hub?
As far as I can tell the answer is six. The following
diagram illustrates the configuration:

Immobilization with six struts
Related work
According to the book: King of Infinite Space: Donald Coxeter, the Man Who Saved Geometry,
by Siobhan Roberts, Fuller:
"made awkward geometrical mistakes such as how many
spokes are needed on a wheel to hold it rigid (Fuller said
12 instead of 7)"
The reference given is to an interview with
Walter Whiteley.
It is nice to see that someone else agrees with the figure
of seven for the number of tensile elements required - and
that they also reached the conclusion that this was one of
Fuller's mistakes.
I published my conclusions in the area about six months
before the book was published - but it seems fairly
likely that these conclusions were reached independently.
Links
My wheel stability is
essay related to this one.
It contains photographs of a bicycle wheel with seven spokes.
Tim Tyler |
Contact |
http://hexdome.com/
|