
HexDome
Hexagonal Geodesic Domes
Wheel stability
The question of the minimum number of spokes it takes to
stabilise a wire wheel was raised - and answered - by Fuller in Synergetics
(see [640.42] and
[537.04]).
Since then Bob Burkhardt has also investigated the issue.
Bob has published his results
[here].
I recently decided to take a look at the issue.
I constructed a number of six, seven and eight spoke wheels.
Here are photographs of some of them:
Eight spoke wheel

Eight spoke wheel
|
|

Close up of where the spokes meet the hub
|
The eight spoke wheel appears to be fully stable.
There are eight-spoke wheels which can be proven to
be fully stable. However, no proof of stability currently
exists for the configuration pictured here.
This configuration seems stable enough - and looks
relatively attractive in the context of a drive wheel.
Seven spoke wheel

Seven spoke wheel
|
|

Close up of where the spokes meet the hub
|
According to my page on the subject,
seven cables is the minimum necessary to produce linear stability when
stabilising a hub in space.
My research indicates that the same figure applies to
bicycle wheels - so here is a seven spoke bicycle wheel.
The design was inspired by a six spoke wheel with radial
spokes.
The design has five radial spokes.
While I believe this wheel is stable in theory,
demonstrating its stability is actually quite complex - and
unfortunately an exposition on why this wheel is
stable is beyond my scope at the moment.
Six spoke wheel

Six spoke wheel
|
|

Close up of where the spokes meet the hub
|
This six spoke wheel has radial spokes.
Like other wheels with radial spokes, it lacks linear stability.
However, it is still usable as a front bicycle wheel -
provided that disc brakes are not used.
Some other of the wheels I have constructed are visible
here.
Degrees of freedom arguments
This page notwithstanding, the original view - that twelve
spokes are required to construct a stable wheel - still
seems to be quite persistent.
Fuller presents his supporting argument for this on:
Synergetics 401.05.
Unfortunately, the argument is incoherent.
There seems to be a hand-waving argument which suggests that
you need two tensile elements to restrain each degree of
freedom present in a dynamical system.
A single solid object in space has six degrees of freedom,
three translational, and three rotational; therefore - one
might think - it needs twelve tensile elements to stabilise
it.
However the argument doesn't seem to withstand close
inspection. In fact, you can prevent a point in space from
moving using four tendons, arranged in the directions of the
points of a surrounding tetrahedron - not the six which the
"degrees of freedom" argument would suggest.
Another argument producing the "twelve" figure suggests
that it takes four forces to immobilise a point.
Then - to stop any sort of movement - you need to immobilise
three points - and three times four is twelve.
If proceeding by immobilising points, this argument is
correct. However there's no constraint that the forces
needed to immobilise an object should be able to be broken
down into groups of forces, each of which immobilise a
point.
There are other ways of immobilising an object.
Consider an object which has already had its translational
degrees of freedom taken away from it - perhaps with four
tensile elements. Are another eight forces really
needed to stop it rotating? The answer is clearly "no". To
illustrate this, rotation can be prevented by preventing
movement around each possible axis of rotation, of which
there are three; resulting in six more forces - and not
eight.
Each axis could be stabilised by two tendons - as shown in
this diagram:
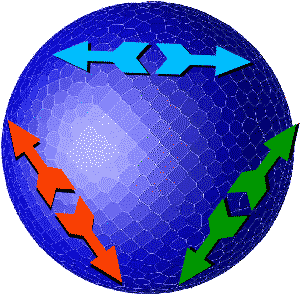
Force diagram showing a way of preventing sphere from
rotating
Notice that these forces are not arranged in such a
way that they can be broken down into groups of four forces
- where each group has the effect of immobilising a single
point. Instead the forces act together synergetically.
Cube stabilised with eight cables

Symbolic representation of stabilised cube
This is a more abstract diagram. The cube in this configuration
can be fairly easily shown to have linear stabilty by a process
involving resolving forces and moments.
One more diagram
Even after reading the original version of this page, some
people still defended Fuller's views on the
subject.
Here's one more attempt at illuminating the mistake:

A simple diagram
Here is a simple diagram of a wheel rim, a strut and six
cables - all of which are the same length.
Because this structure is so simple it should be fairly easy
for people to understand its behaviour intuitively.
The strut in this photograph has lost five of its original
six degrees of freedom.
It can't move up down, left, right or in and out.
Two of its rotational degrees of freedom are also gone.
The only remaing way in which it is free to move is
by rotating about an axis along its length.
Now if Fuller was right about twelve cables
being needed to immobilise an object in space, it should
take another six cables to finally immobilise that
central strut. I hope that conclusion is clearly mistaken
to everyone.
Links
My minimal stable
system is essay related to this one.
The stability essay is also relevant.
Tim Tyler |
Contact |
http://hexdome.com/
|