
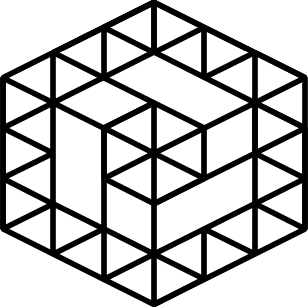
HexDome
Hexagonal Geodesic Domes
Triangulation
The notion of being "fully triangulated" is often invoked in
discussions of the stability of systems.
It is possible to describe algorithms to categorise
structures according to whether they are fully triangulated
or not. Such classifications often have some utility when
determining the stability of systems.
Here is one such algorithm. It tries to classify as many
stable objects as it can easily manage as being "fully
triangulated":
An algorithm that categorises systems according to
whether they are fully triangulated
The following algorithm categorises hub and strut systems
where struts cannot overlap other struts.
Define a strut as being a solid object.
- For each solid object
a in the system consider
if it is attached to two other solid objects b
and c in such a way that b is also
attached to c.
If so, a, b and c
form a single new soild object.
- Otherwise for each solid object
a in the system
consider if it is attached to another other solid object
b in at two (or more) places.
If so, a and b form a single new
soild object.
Repeat the above two steps until there no more solid objects
can be formed.
At the end of the process there will be zero or more solid
objects in the system. If there is precisely one solid
object the system is defined as being fully
triangulated.
Illustrations:

Three composite solid objects forming a triangle
Two composite solid objects joined in two places
A composite solid object forming a triangle with two struts
Fully triangulated systems
What can be said about 2D systems which are fully triangulated?
All such structures are stable. They all have linear stability.
Structures which are not fully triangulated may be either stable or unstable.
Here are some examples of 2D structures which are not fully
triangulated - but are still stable:
Not fully triangulated - but still stable
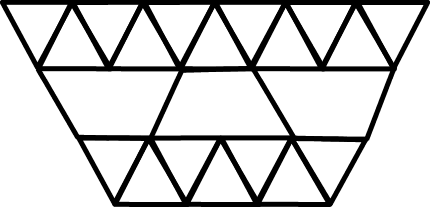
Not fully triangulated - but still stable
Further extensions
Can the notions so far discussed be extended further, so that more
objects are correctly identified as conclusively stable?
Probably.
The next most obvious extension to the existing definition
states that if two solid objects are connected together by
three solid objects, where each of the three objects has an
associated line through their respective "points of
attachment"; and those lines are not all parallel; and those
lines don't all intersect at the same point - then the
resulting composite object is also stable.
The implications of this rule need further exploration.
3D
What is the significance of triangulation in 3D?
Much the same algorithm can be applied to three dimensional
structures.
However it is no longer true that all fully trigangulated
structures are stable.
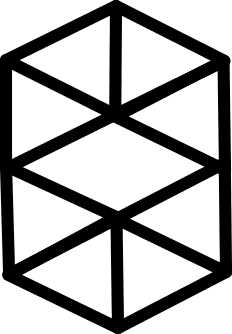
As an example of a fully-triangulated structure that lacks
stability, consider the flexahedron:

Flexahedron - fully triangulated, but unstable
As with the 2D case, structures which are not fully triangulated may
also be stable or unstable.
More useful concepts for use in 3D
Since triangulation is not very useful in determining stability in
systems in 3D, are there more useful concepts, that allow conclusions
to be drawn about the stability of 3D structures?
One approach is to consider structures with clearly-defined surfaces.
If such a surface exists, and it forms a convex hull, then
full triangulation of the surface implies stability of the
resulting structure.
There are other results along similar lines.
Another approach involves concepts such as tetrahedralization.
Instead of considering if an object is joined to two other
objects that are themselves linked, tetrahedralization
requires an object be linked to three other solid
objects - that are themselves all linked to each other.
Constraints are needed to ensure linear stability - no
three points of attachment should lie in a straight line.
All fully tetrahedralized structures are linearly stable.
A flexahedron does not qualify as tetrahedralized under such
a definition.
The notion of tetrahedralized may be extended by permitting
extensions using octahedra, icosahedra, decahedra - and
the other primitive stable three dimensional structures.
However that exercise is beyond the scope of this essay.
As with lack of triangulation, lack of tetrahedralization
does not imply anything about stability.
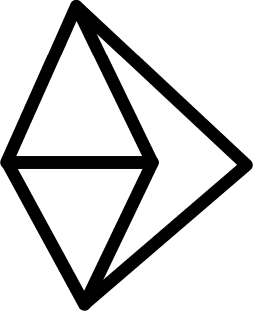
Here is a stable structure which is not triangulated or
tetrahedralized. Nor is it clearly a composite of other
stable polyhedra:

This structure is stable
Tim Tyler |
Contact |
http://hexdome.com/
|