Hexagonal Geodesic Domes

Stability

The term stability usually refers to whether something maintains its state in the face of small perturbations.

In the context of static mechanical systems, it is conventional to consider stability in terms of the response of the system to small spatial displacements of its component parts.

Assessing stability

• Empirical assessment typically consists of building or simulating the structure, subjecting the result to small perturbations - and looking at how it responds.

• Analytical assessment usually involves an examination of the equations of motion that govern the forces on an abstract model of a structure when it is perturbed.

Types of stability

There are static and dynamic stability. A gyroscope can have a type of stability when in motion which would not show up in a static stability analysis of its components. This essay will only deal with static stability.

There's asymptotic stability, and Lyapounov stability:

• Lyapounov stability refers to systems where the system remains in a neighbourhood of the equilibrium position after perturbation.

• Asymptotic stability describes systems where equilibrium is increasingly closely approached after a perturbation.

Then there's linear and non-linear stability:

• Linear stability analysis takes a first order approximation of the differential equations governing motion - by simply discarding higher order terms from their Taylor series expansion - and considers the stability of the resulting simplified system.
• If a system lacks linear stability, non-linear analysis may still find it exhibits a kind of stability after higher order terms are considered.

Linear stability analysis

The main idea behind this approach is to simplify the analysis - and get a reasonable quality answer quickly.

Often a linear stability analysis will tell you most of what you need to know about the stability of a structure.

If the resulting linear system is stable - and the restoring forces are large enough - consideration of higher order terms is unlikely to add much to the conclusion.

On the other hand, a system which is not linearly stable is likely to have some sort of stability problem - even if analysis of higher order terms indicated that there is still a type of of non-linear stability present.

A diagram should help illustrate the notion of linear stability:

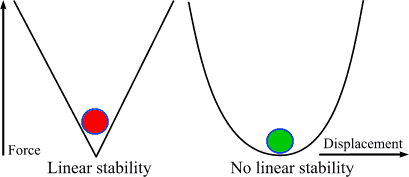
Linear stability in a nutshell

The red ball illustrates a system with linear stability. Any perturbation results in a force which acts to restore the stable position. The magnitude of the force is proportional to the distance moved through.

The green ball illustrates a system lacking linear stability. While displacements do result in forces that act to restore the stable position, smaller perturbations result in disproportionally smaller restoring forces - and the first derivitave of force with respect to displacement is zero.

In other words, the limit of dF/dx as x -> 0 (where x is a measure of displacement, and F is the magnitude of the resultant force) is zero.

Linear stability is sometimes known as "first order stability".

In the terminology of rigidity theory, "linear stability" refers to the shared property of those networks which are rigid, and which lack infinitesimal rigidity.

Vibrations

This is a quite general phenomenon: systems lacking linear stability are prone to oscillations and vibrations.

A classic example of a system lacking linear stability is a guitar string.

Small perturbations change the string's length only slightly

There a small transverse perturbation results in a restoring force proportion to the degree to which the string has been extended, which goes roughly according to the it's the cosine of the angle it has been moved through, minus one.

The Taylor expasion of Cosine goes: cos(x) = 1 - x^2/2 + x^4/24...

Subtract one and you get a restoring force which is proportional to:x^2/2 - x^4/24 - an expression which has no linear term.

Consequently a guitar string is relatively free to exhibit small oscillations - since there is practically no restoring force opposing such small scale movements.

The result is a system which is prone to small-scale vibrations.

Linear stability - example

Radial spokes result in a wheel which is not linearly stable

Here the hub resists translational movements - but presents little resistance to small perturbations which rotate the rim about it's own axis while holding the hub still.

In this example, with an angular perturbation of Theta, the limit of dForce/dTheta - as Theta tends towards zero - is zero.

Such a layout would be especially bad in a rear driving wheel - or in a wheel equipped with a disc brake.

The bicycle illustrated above has no disc brakes - and uses a different configuration of spokes in its rear wheel.

Non-linear stability analysis

The non-linear forces may increase rapidly enough for them to be effective at keeping the system near the stable state.

Alternatively, oscillations may not matter:

In the example of the bicycle wheel, the oscillations are of the hub, with respect to the rim. However, such oscillations do not have much functional effect in the context of such a wheel. They may perhaps accelerate the progress of metal fatigue in the spokes - but spokes have to resist such forces anyway: they are a natural part of the normal function of the wheel.

Similarly systems which do have linear stability may have restoring forces which are too weak for them to be effective at maintaing structural stability in the face of perturbations on the scale which can be expected.

In such cases, a more complex analysis may be needed - one that considers more than simply the linear component of the restoring forces.