
HexDome
Hexagonal Geodesic Domes - Catenary Domes
Resisting gravity
Hexagonal structures are not stable - and need stabilising.
However, the volume of stabilising material needed can be minimised.
At first, I thought that this would prove to be a challenging optimisation
problem. However the problem of how to build a maximally stable hexagonal
surface in a gravitational field turned out to have a beautiful solution.
Catenary
Catenary is the name given to the curve formed by a cable
supported at its ends in a gravitational field. Catenary
curves resemble - but are different from - parabolas.
Catenary curves are though to form highly stable arches.
The reason can be seen by an examination of the following force diagrams:
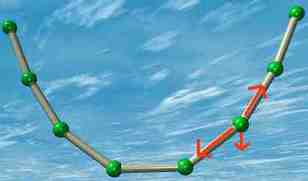
In tension
|
|
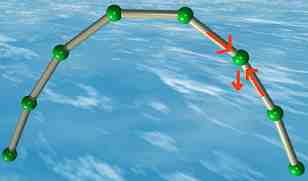
Under compression
|
These force diagrams resolve forces at a single node. There are forces applied
by either strut - and a force applied to the node due to gravity.
When hanging under gravity, a catenary curve is formed. At this point, all the
nodes are stationary - and consequently all the forces balance.
Next the entire structure is inverted.
Assuming the struts are more-or-less incompressible, then all the forces will
be precisely reversed as well - and all the forces will still exactly balance -
resulting in no resultant force being applied to any of the nodes.
The resulting configuration may not be stable - but
it should be exactly balanced - a similar situation
to a pencil balanced on its point.
Domes
Exactly the same principle that applies to arches also applies to domes.
Catenary dome gallery
I've constructed a catenary dome gallery - to
illustrate some of the associated shapes and construction principles.
Other considerations
Catenary domes are optimal as far as resisting gravity goes. However domes have to
do other things besides resist gravity. In particular, they need to resist wind
forces and external impacts. More uniform curvature than is present in a typical
caterary dome might help with such applications.
There are a number of possible ways of compromising between uniform curvature
and a true catenary dome.
These include performing a simulation with a relatively inflexible material,
and modelling inflating the dome.
Tim Tyler |
Contact |
http://hexdome.com/
|